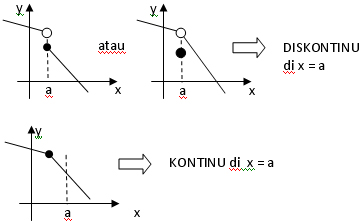
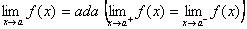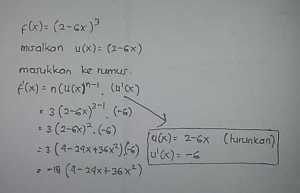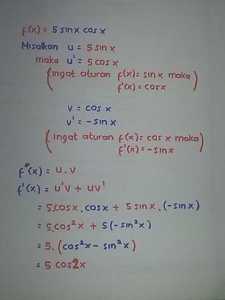22DEC
Rumus-rumus Dasar Turunan
Rumus-rumus berikut dapat dibuktikan dengan definisi turunan (Definisi 5.2), dan biasa disebut rumus-rumus dasar turunan:
y = k y’ = 0 , ” konstanta k Fungsi konstan
y = kxn y’ = knxn-1, ” konstanta k
y = sin x
y = cos x y’ = cos xy’ = – sin x Fungsi Trigonometri
y = ex y’= ex Fungsi eksponensial
Tabel 6.1.
Bukti :
Berikut beberapa bukti rumus-rumus dasar :
Ø Rumus dasar no. 4., jika y = cos x maka
y’ = ==
= = 0 – sin x = – sin x.
Ø Rumus dasar no 7., jika y = ex maka :
y’ = =
= =
=
Dengan menggunakan aturan turunan (teorema 5.2 atau 5.3), dapat dicari turunan fungsi trigonometri, fungsi hiperbolik yang belum ada di table 6.1., seperti :
Fungsi Trigonometri :
y = tg x
y = ctg x
y = sec x
y = cossec x y’ = sec2xy’ = – cossec2xy’ = sec x tg x
y’ = – cossec x ctg x
Fungsi hiperbolik
y = sinh x
y = cosh x
y = tgh x
y = ctgh x
y = sech x
10. y = cossech x y’ = cosh xy’ = sinh xy’ = sech2x
y’ = cossech 2x
y’ = sech x tgh x
y’ = cossech x ctgh x
Tabel 6.2.
Turunan fungsi-fungsi di atas tidak perlu dihafal karena dengan mudah dapat diperoleh fungsi turunannya. Di bawah ini diberikan beberapa bukti dari table 6.2., sebagai berikut :
Ø Bukti no. 2., y = ctg x = maka dengan aturan hasil bagi diperoleh :
y’ =
Ø
Ingat Kembali !!
sinh x = ; cosh x =
Bukti no. 5, y = sinh x =
maka dengan aturan jumlah, diperoleh :
y’ = = cosh x
Ø Bukti no. 7., y = sech x = 1/cosh x, maka dengan aturan hasil bagi diperoleh :
y’ =
Turunan fungsi polynomial dan fungsi rasional juga sering menggunakan aturan turunan pada teorema 5.2 atau 5.3. coba perhatikan contoh berikut :
Dengan menggunakan aturan turunan, tentukan y’ dari fungsi-fungsi berikut :
1). y = x3cos x 2). y = 3). y =
Jawab :
1). y = x3cos x maka dengan aturan hasil kali diperoleh :
y’ = 3x2cos x + x3(-sin x) = 3x2cos x – x3sin x = x2 (3cos x – x sin x)
2). y = maka dengan aturan hasil bagi diperoleh :
y’ =
3). y = maka dengan aturan hasil bagi diperoleh :
y’ =
=
Aturan Rantai
Teorema 6.1. : Aturan Rantai
Jika fungsi y = f(u) & u = g(x) menentukan fungsi komposisi y = f(g(x)) = (f◦g) (x), sedangkan g terdifferensialkan di x dan f terdifferensialkan di u = g(x) maka fungsi komposisi f◦g terdifferensialkan di x, yakni :
(f◦g)’ (x) = f ’(g(x)) g’(x) atau Dxy = DuyDxu atau =
Catatan :
1. Jika y = f1(u1), u1 = f 2(u2), u2 = f3(u3), …, un-1 = fn(un), un=fn(x) maka
y’ = =
2. Fungsi bentuk parameter merupakan fungsi y = f(x) yang disajikan dengan sepasang persamaan : dengan t suatu parameter, maka untuk memperoleh dari system persamaan tersebut adalah dengan diasumsikan y sebagai fungsi komposisi :
y = f(t), t = g(x), berarti : = atau =
Dengan aturan rantai, tentukan fungsi-fungsi berikut :
1). y = 2). y = 3). y =
Jawab :
1). y = ,
dimisalkan y = , u = maka = =
2). y = , dimisalkan y = v2, v = cos w, w = 4x maka
= = 2v(-sin w)4 = -2.4.cos4x.sin4x = -4sin 8x
3). y = , dimisalkan y = u3, u = sin v, v = w7, w = x2 – 3x, maka :
= = 3u2.cos v. 7w6.(2x-3)
= 3.7(x2 – 3x )6.(2x-3)
= 21(x2 – 3x )6.(2x-3).
= (x2 – 3x )6.(2x-3)